Tam giác vuông là một loại hình học cơ bản và phổ biến trong toán học. Hiểu rõ cách tính diện tích tam giác vuông là điều cần thiết cho việc giải các bài toán hình học, ứng dụng vào thực tế, và nâng cao kiến thức toán học. Bài viết này sẽ cung cấp một cách tổng quát về công thức tính diện tích tam giác vuông cũng như các ví dụ minh họa, bài tập thực hành liên quan đến diện tích tam giác vuông.
Ví dụ minh họa về diện tích tam giác vuông
1. Tam giác vuông có hai cạnh góc vuông bằng 5 cm và 12 cm
- Bước 1: Xác định hai cạnh góc vuông:
- Cạnh góc vuông thứ nhất: 5 cm
- Cạnh góc vuông thứ hai: 12 cm
- Bước 2: Áp dụng công thức tính diện tích tam giác vuông:
- Diện tích = (Cạnh góc vuông thứ nhất * Cạnh góc vuông thứ hai) / 2
- Diện tích = (5 cm * 12 cm) / 2
- Diện tích = 30 cm²
- Kết luận: Diện tích tam giác vuông là 30 cm²
2. Tam giác vuông có một cạnh góc vuông bằng 8 cm và diện tích bằng 24 cm²
- Bước 1: Xác định cạnh góc vuông đã biết:
- Cạnh góc vuông thứ nhất: 8 cm
- Bước 2: Áp dụng công thức tính diện tích tam giác vuông để tìm cạnh góc vuông còn lại:
- Diện tích = (Cạnh góc vuông thứ nhất * Cạnh góc vuông thứ hai) / 2
- 24 cm² = (8 cm * Cạnh góc vuông thứ hai) / 2
- Cạnh góc vuông thứ hai = (24 cm² * 2) / 8 cm
- Cạnh góc vuông thứ hai = 6 cm
- Kết luận: Cạnh góc vuông còn lại của tam giác vuông là 6 cm
3. Tam giác vuông có cạnh huyền bằng 13 cm và một cạnh góc vuông bằng 5 cm
- Bước 1: Áp dụng định lý Py-ta-go để tìm cạnh góc vuông còn lại:
- Cạnh huyền² = Cạnh góc vuông thứ nhất² + Cạnh góc vuông thứ hai²
- 13² = 5² + Cạnh góc vuông thứ hai²
- Cạnh góc vuông thứ hai² = 13² – 5²
- Cạnh góc vuông thứ hai = √(13² – 5²) = √(169 – 25) = √144 = 12 cm
- Bước 2: Áp dụng công thức tính diện tích tam giác vuông:
- Diện tích = (Cạnh góc vuông thứ nhất * Cạnh góc vuông thứ hai) / 2
- Diện tích = (5 cm * 12 cm) / 2
- Diện tích = 30 cm²
- Kết luận: Diện tích tam giác vuông là 30 cm²
Bài toán liên quan đến diện tích tam giác vuông
1. Cho tam giác vuông ABC vuông tại A, AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ABC.
- Bước 1: Xác định hai cạnh góc vuông:
- AB = 6 cm
- AC = 8 cm
- Bước 2: Áp dụng công thức tính diện tích tam giác vuông:
- Diện tích = (AB * AC) / 2
- Diện tích = (6 cm * 8 cm) / 2
- Diện tích = 24 cm²
- Kết luận: Diện tích tam giác vuông ABC là 24 cm²
2. Cho tam giác vuông MNP vuông tại M, MN = 10 cm, diện tích tam giác MNP bằng 30 cm². Tính độ dài cạnh MP.
- Bước 1: Áp dụng công thức tính diện tích tam giác vuông:
- Diện tích = (MN * MP) / 2
- 30 cm² = (10 cm * MP) / 2
- Bước 2: Tìm độ dài cạnh MP:
- MP = (30 cm² * 2) / 10 cm
- MP = 6 cm
- Kết luận: Độ dài cạnh MP là 6 cm
3. Cho tam giác vuông XYZ vuông tại X, YZ = 15 cm, diện tích tam giác XYZ bằng 36 cm². Tính độ dài các cạnh XY và XZ.
- Bước 1: Áp dụng định lý Py-ta-go để tìm mối quan hệ giữa XY và XZ:
- XY² + XZ² = YZ²
- XY² + XZ² = 15²
- XY² + XZ² = 225
- Bước 2: Áp dụng công thức tính diện tích tam giác vuông:
- Diện tích = (XY * XZ) / 2
- 36 cm² = (XY * XZ) / 2
- Bước 3: Giải hệ phương trình gồm hai phương trình thu được ở Bước 1 và Bước 2 để tìm XY và XZ. Phương trình thứ hai có thể viết lại thành: XY * XZ = 72
- Bước 4: Tìm nghiệm của hệ phương trình. Ta có thể giải hệ phương trình bằng cách thế hoặc bằng cách sử dụng máy tính.
- Kết luận: Độ dài các cạnh XY và XZ là … cm (giải hệ phương trình để tìm ra kết quả cụ thể).
Tính chất của tam giác vuông
1. Tổng ba góc trong tam giác vuông bằng 180°
- Chứng minh:
- Trong tam giác vuông, một góc bằng 90°.
- Tổng hai góc nhọn còn lại bằng 180° – 90° = 90°.
- Vậy, tổng ba góc trong tam giác vuông bằng 90° + 90° = 180°.
- Ứng dụng:
- Sử dụng tính chất này để tìm số đo các góc còn lại trong tam giác vuông khi biết một góc.
- Chứng minh các tính chất liên quan đến tam giác vuông.
2. Định lý Py-ta-go
- Nội dung: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
- Với tam giác vuông ABC vuông tại A, ta có: BC² = AB² + AC²
- Chứng minh: Định lý Py-ta-go có nhiều cách chứng minh khác nhau, bao gồm chứng minh bằng hình học, đại số, và lượng giác.
- Ứng dụng:
- Tìm độ dài một cạnh trong tam giác vuông khi biết độ dài hai cạnh còn lại.
- Chứng minh các tính chất liên quan đến tam giác vuông.
- Giải các bài toán hình học, đặc biệt là các bài toán về độ dài, diện tích, chu vi trong tam giác vuông.
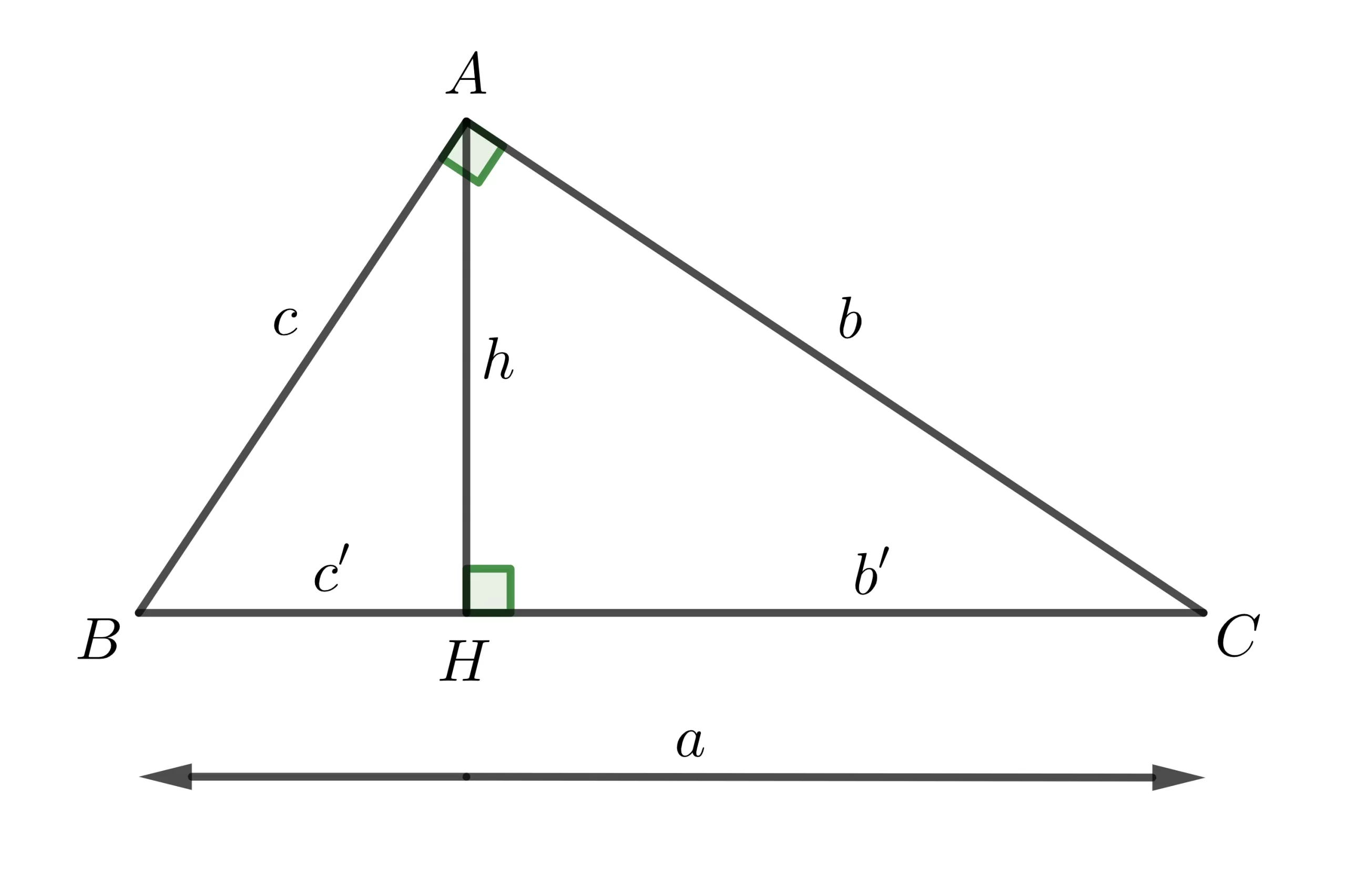
3. Các đường cao trong tam giác vuông
- Đường cao: Đường cao trong tam giác vuông là đường thẳng kẻ từ đỉnh góc vuông đến cạnh huyền.
- Tính chất:
- Đường cao chia tam giác vuông thành hai tam giác vuông nhỏ hơn, đồng dạng với tam giác lớn.
- Độ dài đường cao là trung bình nhân của hai đoạn thẳng mà đường cao chia cạnh huyền.
- Độ dài cạnh huyền là trung bình nhân của hai cạnh góc vuông.
- Ứng dụng:
- Tìm độ dài các cạnh và đường cao trong tam giác vuông.
- Chứng minh các tính chất liên quan đến tam giác vuông.
- Giải các bài toán hình học, đặc biệt là các bài toán về độ dài, diện tích, chu vi trong tam giác vuông.
Ứng dụng của diện tích tam giác vuông trong thực tế
1. Xây dựng và kiến trúc
- Tính diện tích tường, mái nhà, cửa sổ, nền nhà: Trong việc xây dựng và kiến trúc, diện tích tam giác vuông được sử dụng để tính toán diện tích các phần tử hình học trong công trình, từ đó giúp cho việc dự toán vật liệu, lựa chọn vật liệu phù hợp, và tối ưu hóa chi phí.
- Lựa chọn kích thước cửa, sửa chữa nhà: Khi thiết kế và xây dựng, cần lựa chọn kích thước cửa, sửa chữa nhà sao cho phù hợp với diện tích và cấu trúc của ngôi nhà. Diện tích tam giác vuông được sử dụng để tính toán kích thước tối ưu cho các phần tử này.
2. Nông nghiệp
- Tính diện tích đất trồng: Diện tích tam giác vuông được sử dụng để tính diện tích đất trồng trong các khu vườn, ruộng bậc thang, giúp cho việc quản lý đất đai, phân bổ giống cây trồng, và tối ưu hóa năng suất.
- Tính khối lượng phân bón: Diện tích tam giác vuông được sử dụng để tính toán khối lượng phân bón cần sử dụng cho mỗi khu vực trồng trọt, giúp cho việc sử dụng phân bón hiệu quả, tiết kiệm chi phí, và bảo vệ môi trường.
3. Địa lý và bản đồ
- Tính diện tích các khu vực: Diện tích tam giác vuông được sử dụng để tính toán diện tích các khu vực trên bản đồ, giúp cho việc phân tích, nghiên cứu về địa lý, môi trường, và các vấn đề liên quan.
- Xác định vị trí: Diện tích tam giác vuông được sử dụng để xác định vị trí của các điểm trên bản đồ, giúp cho việc định vị, định hướng, và điều hướng, đặc biệt là trong lĩnh vực hàng hải, hàng không.
Cách đo và tính diện tích tam giác vuông
1. Dụng cụ đo
- Thước kẻ: Dùng để đo độ dài các cạnh của tam giác vuông.
- Thước đo góc: Dùng để đo số đo các góc của tam giác vuông.
- Máy tính: Dùng để thực hiện các phép tính toán.
2. Cách đo
- Đo độ dài hai cạnh góc vuông bằng thước kẻ.
- Đo số đo góc vuông bằng thước đo góc (thường là 90°).
3. Cách tính diện tích
- Áp dụng công thức tính diện tích tam giác vuông:
Diện tích = (Cạnh góc vuông thứ nhất Cạnh góc vuông thứ hai) / 2
- Thay độ dài hai cạnh góc vuông đã đo vào công thức để tính diện tích.
- Diện tích được đo bằng đơn vị diện tích, ví dụ: cm², m², km².
Bài toán tính diện tích tam giác vuông trong hình học
1. Cho hình chữ nhật ABCD có AB = 6 cm, AD = 8 cm. Tính diện tích tam giác ABC.
- Phân tích: Tam giác ABC là một tam giác vuông tại A, có AB = 6 cm và AC = AD = 8 cm.
- Giải: Áp dụng công thức tính diện tích tam giác vuông:
Diện tích = (AB AC) / 2 = (6 cm * 8 cm) / 2 = 24 cm²
- Kết luận: Diện tích tam giác ABC là 24 cm².
2. Cho hình bình hành MNPQ có MN = 10 cm, MQ = 8 cm, góc MNP = 90°. Tính diện tích tam giác MNQ.
- Phân tích: Tam giác MNQ là một tam giác vuông tại M, có MN = 10 cm và MQ = 8 cm.
- Giải: Áp dụng công thức tính diện tích tam giác vuông:
Diện tích = (MN MQ) / 2 = (10 cm * 8 cm) / 2 = 40 cm²
- Kết luận: Diện tích tam giác MNQ là 40 cm².
3. Cho hình vuông ABCD có cạnh bằng 5 cm. Tính diện tích tam giác ABD.
- Phân tích: Tam giác ABD là một tam giác vuông tại A, có AB = AD = 5 cm.
- Giải: Áp dụng công thức tính diện tích tam giác vuông:
Diện tích = (AB AD) / 2 = (5 cm * 5 cm) / 2 = 12,5 cm²
- Kết luận: Diện tích tam giác ABD là 12,5 cm².
Sự liên quan giữa cạnh và diện tích tam giác vuông
1. Tỉ lệ thuận
- Diện tích tam giác vuông tỉ lệ thuận với bình
- Nếu tăng độ dài một cạnh góc vuông lên n lần, diện tích tam giác tăng lên n² lần.
- Nếu giảm độ dài một cạnh góc vuông đi n lần, diện tích tam giác giảm đi n² lần.
2. Ảnh hưởng của cạnh huyền
- Diện tích tam giác vuông phụ thuộc vào độ dài cạnh huyền
- Nếu tăng độ dài cạnh huyền, diện tích tam giác vuông cũng tăng.
- Nếu giảm độ dài cạnh huyền, diện tích tam giác vuông cũng giảm.
- Tuy nhiên, không có mối quan hệ tuyến tính trực tiếp giữa diện tích tam giác vuông và độ dài cạnh huyền.
3. Ứng dụng
- Tìm diện tích tam giác vuông khi biết tỉ lệ thay đổi cạnh:
- Ví dụ: Nếu một cạnh góc vuông của tam giác vuông tăng lên gấp đôi, diện tích tam giác sẽ tăng lên gấp 4 lần (2² = 4).
- Xây dựng các công thức tính diện tích dựa trên tỉ lệ:
- Ví dụ: Nếu một cạnh góc vuông của tam giác vuông tăng lên gấp 3 lần, diện tích tam giác sẽ tăng lên gấp 9 lần (3² = 9).
Diện tích tam giác vuông so với các loại tam giác khác
1. Tam giác đều
- Diện tích tam giác đều bằng một nửa tích cạnh và đường cao.
- Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
- So sánh:
- Diện tích tam giác đều và tam giác vuông có thể bằng nhau hoặc khác nhau, tùy thuộc vào kích thước của các cạnh.
2. Tam giác cân
- Diện tích tam giác cân bằng một nửa tích cạnh đáy và đường cao.
- Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
- So sánh:
- Diện tích tam giác cân và tam giác vuông có thể bằng nhau hoặc khác nhau, tùy thuộc vào kích thước của các cạnh.
3. Tam giác thường
- Diện tích tam giác thường bằng một nửa tích đáy và chiều cao tương ứng.
- Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
- So sánh:
- Diện tích tam giác thường và tam giác vuông có thể bằng nhau hoặc khác nhau, tùy thuộc vào kích thước của các cạnh.
Bài toán ứng dụng diện tích tam giác vuông
1. Một mảnh đất hình chữ nhật có chiều dài là 20 mét, chiều rộng là 15 mét. Người ta xây một ngôi nhà có hình tam giác vuông trên mảnh đất. Cạnh góc vuông thứ nhất của ngôi nhà là 10 mét, cạnh góc vuông thứ hai là 8 mét. Tính diện tích phần đất còn lại sau khi xây nhà.
- Phân tích:
- Diện tích mảnh đất: 20 mét * 15 mét = 300 m²
- Diện tích ngôi nhà: (10 mét * 8 mét) / 2 = 40 m²
- Diện tích đất còn lại: 300 m² – 40 m² = 260 m²
- Kết luận: Diện tích phần đất còn lại sau khi xây nhà là 260 m².
2. Một tấm bìa hình tam giác vuông có diện tích là 24 cm². Cạnh góc vuông thứ nhất dài 6 cm. Tính độ dài cạnh góc vuông thứ hai.
- Phân tích:
- Diện tích = (Cạnh góc vuông thứ nhất * Cạnh góc vuông thứ hai) / 2
- 24 cm² = (6 cm * Cạnh góc vuông thứ hai) / 2
- Giải:
- Cạnh góc vuông thứ hai = (24 cm² * 2) / 6 cm = 8 cm
- Kết luận: Độ dài cạnh góc vuông thứ hai là 8 cm.
3. Một mảnh đất hình tam giác vuông có diện tích là 120 m². Cạnh góc vuông thứ nhất dài 12 mét. Tính độ dài cạnh huyền của mảnh đất.
- Phân tích: Cần tìm độ dài cạnh huyền, chúng ta cần áp dụng định lý Py-ta-go.
- Giải:
- Diện tích = (Cạnh góc vuông thứ nhất * Cạnh góc vuông thứ hai) / 2
- 120 m² = (12 mét * Cạnh góc vuông thứ hai) / 2
- Cạnh góc vuông thứ hai = (120 m² * 2) / 12 mét = 20 mét
- Áp dụng định lý Py-ta-go:
- Cạnh huyền² = Cạnh góc vuông thứ nhất² + Cạnh góc vuông thứ hai²
- Cạnh huyền² = 12² + 20²
- Cạnh huyền = √(12² + 20²) = √(144 + 400) = √544 = 23,32 mét (làm tròn đến 2 chữ số thập phân)
- Kết luận: Độ dài cạnh huyền của mảnh đất là 23,32 mét.
Kết luận
Công thức tính diện tích tam giác vuông là một công cụ hữu ích để giải quyết các bài toán hình học liên quan đến tam giác vuông, ứng dụng vào thực tế, và nâng cao kiến thức toán học. Trong bài viết này, chúng ta đã tìm hiểu về công thức tính diện tích tam giác vuông, các ví dụ minh họa, bài tập thực hành, tính chất của tam giác vuông, ứng dụng của diện tích tam giác vuông trong thực tế, cách đo và tính diện tích tam giác vuông, bài toán tính diện tích tam giác vuông trong hình học, sự liên quan giữa cạnh và diện tích tam giác vuông, diện tích tam giác vuông so với các loại tam giác khác, và bài toán ứng dụng diện tích tam giác vuông. Hy vọng bài viết này của TDMU Language center đã giúp bạn hiểu rõ hơn về diện tích tam giác vuông và có thể áp dụng nó vào các trường hợp cụ thể.

