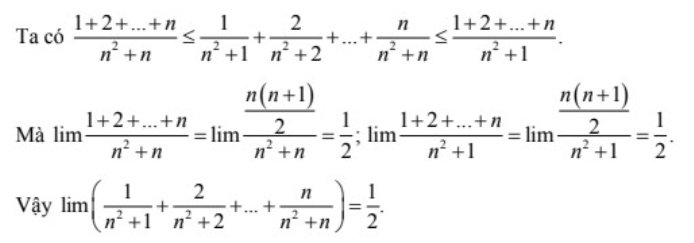1. Lý thuyết giới hạn của dãy số
1.1. Dãy số có giới hạn 0
Định nghĩa: Nếu với mỗi số dương nhỏ tùy ý mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều có giá trị tuyệt đối nhỏ hơn số dương đó thì dãy số (un) đó có giới hạn 0.
Tính chất:
$lim frac{1}{n}=0; limfrac{1}{n^{alpha}}=0(alpha>0); limq^{n}=0(left | q right |<1)$
Định lý:
$u_{n},v{n}:left{begin{matrix} left | u_{n} right | leq v_{n} lim(v_{n})=0 end{matrix}right. Rightarrow lim , u_{n}=0$
1.2. Dãy số có giới hạn hữu hạn
Định nghĩa: Dãy số có giới hạn hữu hạn là dãy số lim (un – L) = 0(L là số thực)
Tính chất:
-
$u_{n}=c$, có giới hạn là c;
-
$lim ,u_{n}=L Leftrightarrow left | u_{n}-L right |$ trên trục số thực từ điểm $u_{n}$ đến L trở nên nhỏ bao nhiêu cũng được miễn là n đủ lớn
Nói một cách hình ảnh khi N tăng thì các điểm $u_{n}$ “chụm lại”
-
Không phải dãy số nào cũng có giới hạn hữu hạn
Định lý:
-
Với $lim(u_{n})=L$ thì ta có định lý:
$limleft | u_{n} right |=left | L right |$ và $limsqrt[3]{u_{n}}=sqrt[3]{L}$.
Nếu $u_{n}geq 0$ với $forall n$ thì $Lgeq 0$ và $limsqrt{u_{n}}=sqrt{L}$
-
Nếu $lim, u_{n}=L, lim, v_{n}=M$ và c là một hằng số thì ta có thể suy ra
$lim(u_{n}+v_{n})=L+M$
$lim(u_{n}-v_{n})=L-M$
$lim(u_{n},v_{n})=LM$
$lim(cu_{n})=cL$
$limfrac{u_{n}}{v_{n}}=frac{L}{M}$(nếu $Mneq 0$)
1.3. Dãy số có giới hạn vô cực
1.3.1. Dãy số có giới hạn $+infty$
Định nghĩa: Nếu với mỗi số dương tuỳ ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều lớn hơn số dương đó thì ta gọi đó là dãy số $(u_{n})$ có giới hạn $+infty$
Hay ta có thể hiểu, $lim , u_{n}=+infty$ trong trường hợp $u_{n}$ có thể lớn hơn một số dương lớn tuỳ ý, kể từ số hạng nào đó trở đi
Tính chất:
$limsqrt{u_{n}}=+infty$
$limsqrt[3]{u_{n}}=+infty$
$lim,n^{k}=+infty$ với một số nguyên dương k cho trước
Trường hợp đặc biệt: $lim , q^{n}=+infty$
$lim , q^{n}=+infty$ nếu q > 1
1.3.2. Dãy số có giới hạn $-infty$
Định nghĩa: Nếu với mỗi số âm tuỳ ý cho trước, mọi số hạng của dãy số, kể từ một số hạng nào đó trở đi, đều nhỏ hơn số âm đó thì ta nói đó là dãy số có giới hạn $-infty$
Ký hiệu: $lim , u_{n}=-infty$
Hay t có thể hiểu, $lim , u_{n}=-infty$ nếu un có thể nhỏ hơn một số âm nhỏ tùy ý.
Tính chất:
$lim, u_{n}=-infty Leftrightarrow lim(-u_{n})=+infty$
Nếu $limleft | u_{n} right |=+infty$ thì un trở nên lớn bao nhiêu cũng được miễn n đủ lớn. Do đó $left | frac{1}{u_{n}} right |=frac{1}{left [ u_{n} right ]}$ trở nên nhỏ bao nhiêu cũng được, miễn n đủ lớn. Nói cách khác, nếu limun=+ thì lim 1un=0
-
Định lý: Nếu $limleft | u_{n} right |=+infty$ thì $limfrac{1}{u_{n}}=0$
2. Các dạng toán về giới hạn của dãy số và ví dụ
2.1. Dạng 1: Tính giới hạn dãy số được cho bởi công thức.
Ví dụ 1: Tìm $lim(n^{3}-2n+1)$?
Lời giải:
Ta có: $n^{3}-2n+1=n^{3}(1-frac{2}{n^{2}}+frac{1}{n^{3}}$
Vì $lim, n^{3}=+infty$ và $lim(1-frac{2}{n^{2}}+frac{1}{n^{3}}=1>0$ nên theo quy tắc 2, $lim(n^{3}-2n+1)=+infty$
Ví dụ 2: Tìm $limsqrt[3]{frac{8n^{2}-3n}{n^{2}}}$
Lời giải:
$limsqrt[3]{frac{8n^{2}-3n}{n^{2}}}=limsqrt[3]{8-frac{3}{n}}=sqrt[3]{8}=2$
Ví dụ 3:
a. Tìm $A=limfrac{2n^{2}+3n+1}{3n^{2}-n+2}$
b. Tìm $B=frac{n^{3}-3n^{2}+2}{n^{4}+4n^{3}+1}$
Lời giải:
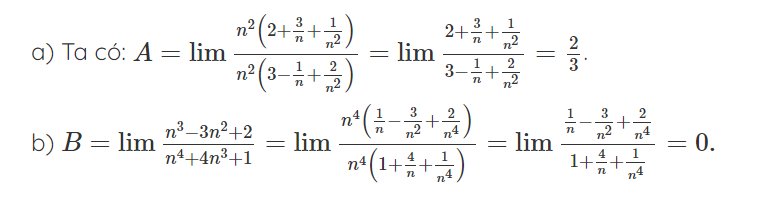
2.2. Dạng 2: Tính giới hạn của dãy số cho bởi hệ thức truy hồi
Ví dụ 1: Cho dãy số $(u_{n})$ được xác định bởi $u_{1}=1, u_{n+1}=frac{2(2u_{n}+1)}{u_{n}+3}$ với mọi n ≥ 1. Biết dãy số $(u_{n})$ có giới hạn hữu hạn, tính $lim, u_{n}$
Lời giải:
Đặt $lim, u_{n}=L Rightarrow L=limfrac{2(2u_{n}+1)}{u_{n}+3}$
$Rightarrow L^{2}-L-2=0Rightarrow L=2$ hoặc L = -1( loại)
Vậy $lim, u_{n}=2$
Ví dụ 2: Cho $(u_{n})$ có $u_{1}=1, u_{n+1}=frac{1}{2}(u_{n}+frac{2}{u_{n}})$ với $forall ngeq 1$. Tìm $lim , u_{n}$?
Lời giải:
Sử dụng phương pháp quy nạp ta chứng minh được $u_{n}>0 forall n$
Tuy đề bài không cung cấp dữ liệu là dãy số $(u_{n})$có giới hạn hữu hạn hay không nhưng nhìn đáp án đề bài cho đều là các giới hạn hữu hạn. Nhớ đó, ta thể khẳng định được dãy số $(u_{n})$ có giới hạn hữu hạn.
Đặt $lim, u_{n}=Lgeq 0$
$lim, u_{n+1}=limfrac{1}{2}(u_{n}+frac{2}{u_{n}})$
Hay $L=frac{1}{2}(L+frac{2}{L})Rightarrow L=frac{2}{L}Rightarrow L^{2}=2Rightarrow L=sqrt{2}$
Vậy $lim, u_{n}=sqrt{2}$
Ví dụ 3: Cho dãy số $(u_{n})$ xác định bởi $u_{1}=1$ và $u_{n+1}=2u_{n}+frac{1}{2}$ với $forall ngeq 1$. Tìm $lim , u_{n}$?
Lời giải:
$v_{n}=u_{n}+frac{1}{2}$. Ta có: $v_{n+1}=u_{n+1}+frac{1}{2}+frac{1}{2}=2u_{n}+frac{1}{2}+frac{1}{2}=2(u_{n}+frac{1}{2})=2v_{n}$
$Rightarrow (v_{n})$ là cấp số nhân có $v_{1}=frac{3}{2}$ và q = 2. Vậy $v_{n}=frac{3}{2}.3^{n-1}=3.2^{n-2}$
Do đó $lim, v_{n}=lim(3.2^{n-2})=+infty$
2.3. Dạng 3: Tính giới hạn của dãy số chứa căn thức
Ví dụ 1: Tính $limsqrt{n^{2}+2n}-n$
Lời giải:
$lim(sqrt{n^{2}+2n-n}=limfrac{(sqrt{n^{2}+2}n)+(sqrt{n^{2}+2n}-n)}{(sqrt{n^{2}+2n}+n)}=limfrac{n^{2}+2n-n^{2}}{sqrt{n^{2}+2n}+n}$
$=limfrac{2n}{sqrt{n^{2}+2n}+n}=lim{2}{sqrt{1+frac{2}{n}}+1}=frac{2}{1+1}=1$
Ví dụ 2: Tính giới hạn của $I=lim(sqrt{n^{2}-2n+3}-n)$
Lời giải:
$I=lim(sqrt{n^{2}-2n+3}-n)$ $=limfrac{(sqrt{n^{2}-2n+3}-n)(sqrt{n^{2}-2n+3}-n)}{sqrt{n^{2}-2n+3}-n}$ $=limfrac{(n^{2}-2n+3)-n^{2}}{sqrt{n^{2}-2n+3}+n}$ $=limfrac{-2n+3}{sqrt{n^{2}-2n+3}+n}$ $=limfrac{-2+frac{3}{n}}{sqrt{1-frac{2}{n}+frac{3}{n^{2}}}+1}$ $=frac{-2}{sqrt{1}+1}=-1$
Ví dụ 3: Tìm $lim(n-sqrt[3]{n^{3}+3n^{2}+1}$
Lời giải:

2.4 Dạng 4: Tính giới hạn của dãy số hữu tỉ
Ví dụ 1: Cho a = 2.151515…, số a còn được biểu diễn dưới dạng $a=frac{m}{n}$, (m,n là các số nguyên dương). m + n =?
Lời giải:
Ta có: $a=2,151515…=2+frac{15}{100}+frac{15}{100^{2}}+frac{15}{100^{3}}+…$
Vì $frac{15}{100}+frac{15}{100^{2}}+frac{15}{100^{3}}+…$ là tổng của csn lùi vô hạn với $u_{1}=frac{15}{100},q=frac{1}{100}$
$Rightarrow a=2+frac{frac{15}{100}}{1-frac{1}{100}}=frac{71}{33}$
Vậy $m=71, n=33 Rightarrow m+n=104$
Ví dụ 2: Bài cho số thập phân vô hạn tuần hoàn có dạng 0,32111… Cũng được viết dưới dạng phân số tối giản là $frac{a}{b}$ (a,b là các số nguyên dương). a – b =?
Lời giải:
Ta có:
$0,3211…=frac{32}{100}+frac{1}{10^{3}}+frac{1}{10^{4}}+frac{1}{10^{5}}+…=frac{32}{100}+frac{frac{1}{10^{3}}}{1-frac{1}{10}}=frac{289}{900}$ Vậy a = 289, b = 900 Do đó, a – b = -611
Ví dụ 3: Tính $limleft [frac{1}{1.3}+frac{1}{3.5}+…+frac{1}{(2n-1)(2n+1)} right ]$
$frac{1}{1.3}+frac{1}{3.5}+…+frac{1}{(2n-1)(2n+1)}=frac{1}{2}(1-frac{1}{3}+frac{1}{3}-frac{1}{5}+….+frac{1}{2n-1}-frac{1}{2n+1})=frac{1}{2}(1-frac{1}{2n+1})$
Vậy $limleft [frac{1}{1.3}+frac{1}{3.5}+…+frac{1}{(2n-1)(2n+1)} right ]=limfrac{1}{2}(1-frac{1}{2n+1})=frac{1}{2}$
2.5 Dạng 5: Tính giới hạn của dãy số chứa lũy thừa – mũ
Ví dụ 1: $limfrac{4^{n+1}+6^{n+2}}{5^{n}+8^{n}}=?$
Lời giải:
$limfrac{4^{n+1}+6^{n+2}}{5^{n}+8^{n}}=limfrac{4(frac{4}{8})^{n}+36(frac{6}{8})^{n}}{(frac{5}{8})^{n}+1}=0$
Ví dụ 2: $limfrac{2^{n}-3^{n}}{2^{n}+1}=?$
Lời giải:
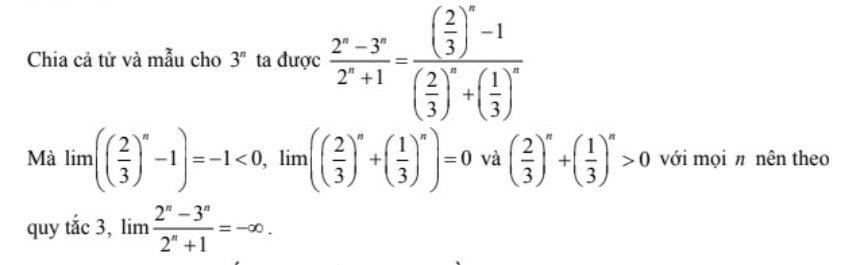
Ví dụ 3: $lim(3.2^{n}-5.3^{n}+7n)=?$
Lời giải: $lim(3.2^{n}-5.3{n}+7n)=3^{n}(-5+6(frac{2}{3})^{n}+7)=-infty$
Đăng ký ngay để được các thầy cô ôn tập và xây dựng lộ trình ôn thi THPT môn Toán sớm đạt 9+
3. Một số bài tập về giới hạn của dãy số từ cơ bản đến nâng cao (Có lời giải)
Ví dụ 1: Xác định các giới hạn cho lưới đây:
a. $limfrac{6n-1}{3n+2}$
b. $limfrac{3n^{2}+n-5}{2n^{2}+1}$
Lời giải:
a. $limfrac{6n-1}{3n+2}=limfrac{n(6-frac{1}{n})}{n(3+frac{2}{n})}=limfrac{6-frac{1}{n}}{3+frac{2}{n}}=frac{6-9}{3-0}=2$
b. $limfrac{3n^{2}+n-5}{2n^{2}+1}=limn23+1n-5n2n23+2n=lim{3+frac{1}{n}-frac{5}{n^{2}}}{2+frac{1}{n^{2}}}=frac{3}{2}$
Ví dụ 2: lim(5n – 2n)
Lời giải:
Ta có: $5^{n}-2^{n}=5^{n}(1-(frac{2}{5}^{n})$
Vì $lim5^{n}=+infty$ và $lim(1-(frac{2}{5}^{n})=1>0$ nên theo quy tắc 2, $lim(5^{n}-2^{n})=+infty$
Ví dụ 3: Tìm lim(3.2n+1 – 5.3n + 7n) =?
Lời giải:
$lim(3.2^{n+1}-5.3^{n}+7n)=3^{n}(-5+6(frac{2}{3})^{n}+7frac{n}{3^{n}}=-infty$ Ví dụ 4: Cho dãy số (un) xác định u1=0, u2=1, un+1=2un-un-1+2 với mọi $ngeq 2$. Tìm lim un?
Lời giải:
Giả sử dãy số trên có giới hạn hữu hạn gọi là L
$Rightarrow lim,u_{n}=2lim,u_{n}-lim,u_{n-1}+2Leftrightarrow L=2L-L+2Leftrightarrow 0=2$ ( Vô lý)
Vậy có thể dự đoán dãy số có giới hạn vô cực. Nhìn vào đáp án ta thấy có hai đáp án vô cực ($-infty$ và $+infty$), vậy chưa thể đoán là đáp án nào. Ta xem hai cách giải sau.
Ta có: u1 = 0, u2 = 1, u3 = 4, u4 = 9. Vậy ta có thể dự đoán un = (n – 1)2 với $forall ngeq 1$. Khi đó,
un+1 = 2un – un-1 +2 = 2(n – 1)2 – (n – 22 + 2) = n2
= [(n – 1) – 1]2
Vậy $u_{n}=(n-1)^{2}$ với $forall ngeq 1$. Do đó, $lim,u_{n}=lim(n-1)^{2}=+infty$
Ví dụ 5: Cho dãy số (un) với $u_{n}=frac{1}{2}-frac{1}{4}+frac{1}{8}+…+frac{(-1)^{n+1}}{2}$. Tìm lim un
Lời giải:
un là tổng n số hạng đầu tiên của một cấp số nhân có $u_{1}=frac{1}{2}$ và $q = frac{-1}{2}$
Do đó $u_{n}=frac{1}{2}.frac{1-(frac{1}{2})^{n}}{1-(frac{1}{2})}=frac{1}{3}(1-(frac{1}{2})^{n}Rightarrow lim,u_{n}=limfrac{1}{3}(1-(frac{1}{2})^{n})=frac{1}{3}$
Ví dụ 6: Tìm $lim, u_{n}$, với $u_{n}=frac{1+2+…+n}{n^{2}+1}$.
Lời giải:
Ta có: $1+2+..+n=frac{n(n+1)}{2}Rightarrow frac{1+2+…+n}{n^{2}+1}=frac{n(n+1)}{2(n^{2}+1)}$
$Rightarrow lim, u_{n}=limfrac{n(n+1)}{2(n^{2}+1)}=frac{1}{2}$
Ví dụ 7: Tìm $limfrac{1+5+9+…+4n-3}{2+7+12+…+5n-3}$
Lời giải:
Tử thức là tổng của n số hạng đầu tiên của cấp số cộng (un) với n = 1, un = 4n -3 và công bội d = 4
Do đó 1+ 5 + 9 +….+ 4n – 3 =
Tương tự ta cũng có 2 + 7 + 12 +…+ 5n – 3 =
Như vậy
Ví dụ 8: Tìm $D=limsqrt{n^{2}+2n}-sqrt[3]{n^{3}+2n^{2}}$
Lời giải:
Ta có:
D =
=
=
Ví dụ 9: Thực hiện trang trí lại ngôi nhà của mình, chú mèo Tom quyết định tô màu một miếng vải hình vuông cạnh bằng 1, mèo Tom tô màu xám các hình vuông nhỏ được đánh số lần lượt là 1, 2, 3,., n,.., Biết cạnh của hình vuông trước gấp đôi cạnh hình vuông sau nó (Giả sử quy trình tô màu của mèo Tom có thể diễn ra vô hạn).
a. Xác định u1,u2,u3 và un
b. Tính lim $S_{n}$ với Sn=u1+u2+u3+…+un
Lời giải:
a. $u_{1}=frac{1}{4}, u_{2}=frac{1}{4}.(frac{1}{4})=frac{1}{4^{2}},…, u_{n}=frac{1}{4^{n}}$
b. $lim S_{n}=lim14+142+…+14n=141-14=13$
Ví dụ 10: Tìm $lim(frac{1}{n^{2}+1}+frac{2}{n^{2}+2}+…+frac{n}{n^{2}+n})$
Lời giải:
Bài viết trên đã giới thiệu cho các em phần lý thuyết cơ bản và các dạng bài về giới hạn của dãy số. Đây là một phần kiến thức khó và quan trọng trong chương trình toán 11 nên để đạt được kết quả tốt nhất các em học cần phải nắm rõ lý thuyết và rèn luyện thêm các dạng bài tập. Các em học sinh có thể truy cập nền tảng Vuihoc.vn và đăng ký tài khoản để luyện đề ngay hôm nay nhé!
Bài viết tham khảo thêm:
- Cấp số nhân
- Cấp số cộng