Trong toán học, hàm Zeta là một trong những khái niệm quan trọng nhất, không chỉ bởi vì nó có rất nhiều tính chất và ứng dụng trong khoa học, mà còn vì những ứng dụng thực tế của nó trong rất nhiều lĩnh vực khác nhau. Trong phần này, chúng ta sẽ cùng tìm hiểu về những ứng dụng của hàm Zeta trong khoa học cũng như thực tiễn.
Ứng dụng của hàm Zeta trong khoa học

Trong toán học, hàm Zeta liên quan đến nhiều chủ đề khác nhau, bao gồm cả lý thuyết số, phương trình vi phân, bất đẳng thức và nhiều lĩnh vực khác. Hàm Zeta cũng được ứng dụng trong các định lý không giải được từ thế kỷ 18 và 19, như định lí cuối cùng của Fermat và giải bài toán số học trên đường cong Elipt
Ứng dụng của hàm Zeta trong thực tiễn

Không chỉ có trong khoa học, hàm Zeta còn có rất nhiều ứng dụng trong thực tiễn. Ví dụ, nó được sử dụng để tính toán các giá trị của dãy số Fibonacci, và cũng được áp dụng trong vật lý, như trong lý thuyết dây và vật lý lượng tử.
Hàm Zeta cũng được ứng dụng trong công nghệ thông tin, như trong mã hóa RSA, và còn được sử dụng trong kinh tế và tài chính, để tính toán các giá trị liên quan đến tài chính như tỷ lệ lợi tức và dòng tiền.
Như vậy, có thể thấy rằng hàm Zeta đóng một vai trò quan trọng trong khoa học và thực tiễn. Trong những phần tiếp theo của bài viết này, chúng ta sẽ tiếp tục tìm hiểu về tính chất của hàm Zeta và những khám phá mới nhất về nó.
Tính chất của hàm Zeta
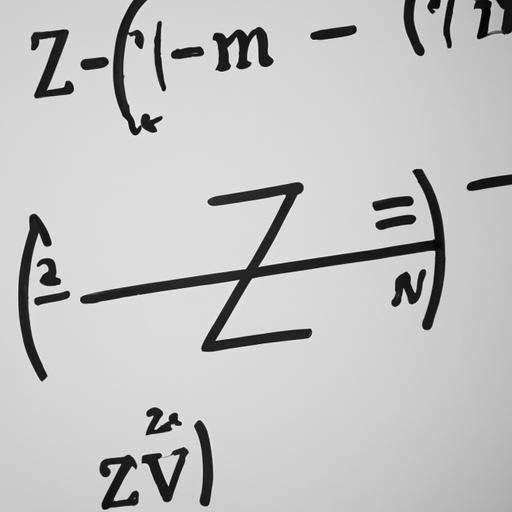
Hàm Zeta có rất nhiều tính chất quan trọng trong toán học và khoa học máy tính. Dưới đây là một số tính chất nổi bật của hàm Zeta:
Tính chất đối xứng:
Hàm Zeta có tính chất đối xứng xung quanh điểm 1/2, có nghĩa là Zeta(s) = Zeta(1 − s). Tính chất này rất hữu ích trong việc tính toán hàm Zeta, và cũng đóng vai trò quan trọng trong các nghiên cứu lý thuyết số.
Tính chất phân tích thành tích:
Hàm Zeta có tính chất phân tích thành tích, nghĩa là những số nguyên tố và số hữu hạn khác nhau đóng góp vào giá trị của hàm Zeta. Tính chất này đóng vai trò quan trọng trong việc tính toán hàm Zeta và nốt ghi chú chồng H)
Ví dụ:
Giá trị của hàm Zeta khi s = 2 là:
Zeta(2) = 1 + 1/2^2 + 1/3^2 + 1/4^2 + 1/5^2 + …
Bằng cách phân tích thành tích, ta có:
Zeta(2) = (1 + 1/2^2 + 1/2^4 + …) x (1 + 1/3^2 + 1/3^4 + …) x (1 + 1/5^2 + 1/5^4 + …) x …
Tính chất liên quan đến số pi:
Một thông tin thú vị về hàm Zeta là nó cho phép tính toán giá trị của số pCụ thể, giá trị của hàm Zeta khi s = 2 liên quan trực tiếp đến giá trị của số pi bằng công thức Zeta(2) = pi^2/6.
Với những tính chất quan trọng này, không khó để hiểu vì sao hàm Zeta lại có vai trò quan trọng trong nhiều lĩnh vực khác nhau của khoa học. Trong những phần tiếp theo của bài viết này, chúng ta sẽ cùng tìm hiểu những khám phá mới nhất về hàm Zeta và cách chúng đóng góp vào lĩnh vực khoa học.
Những khám phá mới về hàm Zeta

Tính chất mới của hàm Zeta
Trong những năm gần đây, có rất nhiều nghiên cứu mới về hàm Zeta, và các nhà khoa học đã tìm ra nhiều tính chất mới của hàm Zeta. Một trong những tính chất mới đó là kết quả của nghiên cứu về định lý Riemann, một trong những định lý lớn nhất trong lý thuyết số. Ở đó, các nhà khoa học đã nhìn thấy mối liên hệ giữa sự phân tán của các số nguyên tố và hàm Zeta.
Sự đóng góp của hàm Zeta trong lĩnh vực tìm kiếm
Những khám phá mới về hàm Zeta cũng đóng góp rất lớn cho lĩnh vực tìm kiếm. Hàm Zeta được sử dụng để tính toán các chỉ số tìm kiếm, nghĩa là số từ khóa mà người dùng sử dụng để tìm kiếm thông tin trên Internet. Các công ty tìm kiếm, như Google và Yahoo, sử dụng hàm Zeta để phân tích tỷ lệ mức độ phổ biến của các từ khóa trên Internet.
Hàm Zeta và ứng dụng trong khoa học
Các nhà khoa học cũng đã áp dụng hàm Zeta trong các nghiên cứu về giải tỏa căng thẳng và cải thiện sức khỏe. Hàm Zeta được liên kết với năng lượng cơ thể và có thể được sử dụng để điều hòa năng lượng trong cơ thể. Ngoài ra, hàm Zeta còn được áp dụng trong lĩnh vực vật lý lượng tử và giải thích các hiện tượng kỳ lạ như việc các hạt vật chuyển động hết sức lạc quan.
Những khám phá mới về hàm Zeta đã mở ra nhiều cánh cửa mới trong khoa học và thực tiễn, và sẽ tiếp tục đóng góp cho sự phát triển của con người trong tương la
Hàm Zeta và sự tự nhiên

Khám phá sự tự nhiên qua hàm Zeta
Hàm Zeta được áp dụng rộng rãi trong nghiên cứu các hiện tượng tự nhiên. Trong toán học, hàm này đóng vai trò quan trọng trong những nghiên cứu về số lướng nguyên tố, trong đó các chuyên gia liên kết tính chất của hàm này với sự phân bổ của các số nguyên tố. Bên cạnh đó, hàm Zeta còn được sử dụng để tính toán các giá trị của các hình học và đường cong, như đường cong Elipti và các hình khối giống nhau.
Liên hệ giữa hàm Zeta và phân tử của thế giới tự nhiên
Hàm Zeta cũng liên quan đến các hiện tượng tự nhiên, chẳng hạn như phân tử của thế giới tự nhiên. Theo các nhà nghiên cứu, đường kính của các phân tử có thể được ước tính bằng cách sử dụng hàm Zeta và các phương trình liên quan. Điều này có thể giúp các nhà khoa học hiểu rõ và dự đoán các tính chất của các phân tử khác nhau và đưa ra phân tích chi tiết hơn về cấu trúc và chức năng của chúng.
Các hiện tượng tự nhiên khác liên quan đến hàm Zeta
Sự tăng trưởng của cây và hàm Zeta
Hàm Zeta cũng được liên kết với sự tăng trưởng của các loài cây trong tự nhiên. Các chuyên gia tin rằng tỷ lệ tăng trưởng của các loài cây có thể được giải thích bởi dãy các số Fibonacci thông qua hàm Zeta. Các nhà toán học cho rằng, đường kính thân cây tăng nhanh hơn so với chiều cao của chúng và sự tăng trưởng này có thể được mô tả bằng một phương trình liên quan đến hàm Zeta.
Sự chênh lệch của sóng âm và hàm Zeta
Hàm Zeta cũng được liên kết đến sự chênh lệch của sóng âm trong tự nhiên. Theo các chuyên gia, hàm điều tiết Zeta có khả năng giải thích sự chênh lệch giữa những địa hình khác nhau trong tự nhiên, ví dụ như sự khác biệt về độ sâu và trơn tru của đáy đại dương đến sự phân bố của các dãy núi và thung lũng trên mặt đất.
Với những ứng dụng tuyệt vời trên, hàm Zeta đang trở thành một trong những khái niệm cơ bản nhất trong khoa học tự nhiên và toán học.
Kết luận
Như vậy, chúng ta đã tìm hiểu về khái niệm hàm Zeta và các tính chất, ứng dụng của nó trong khoa học và thực tiễn. Hàm Zeta đóng một vai trò quan trọng trong nhiều lĩnh vực, từ lý thuyết số đến mã hóa, vật lý và tài chính.
Trong tự nhiên, hàm Zeta được áp dụng để mô tả các hiện tượng như chuyển động ngang của thiên thể, tần số của sóng âm và các thuật toán xử lý tín hiệu.
Với những khám phá mới nhất về hàm Zeta, chuyên gia toán học đang tiếp tục tìm hiểu và khám phá thêm những tính chất mới của nó, không chỉ trong lĩnh vực toán học mà còn trong những lĩnh vực khác như khoa học dữ liệu và trí tuệ nhân tạo.
Tổng kết lại, hàm Zeta là một khái niệm quan trọng và nó có nhiều ứng dụng và tính chất đáng kể trong khoa học và thực tế. Với những tính chất quan trọng này, hàm Zeta được xem là một trong những khái niệm cơ bản của toán học và khoa học máy tính hiện đạ
Tổng kết
Kết luận lại, hàm Zeta là một khái niệm quan trọng trong toán học và có rất nhiều tính chất và ứng dụng trong khoa học cũng như trong thực tiễn. Nó không chỉ liên quan đến nhiều định lý quan trọng, mà còn được sử dụng để tính toán các giá trị trong nhiều lĩnh vực khác nhau như công nghệ thông tin, kinh tế và tài chính.
Việc tìm hiểu về hàm Zeta là một lĩnh vực thú vị và có thể mở ra rất nhiều cánh cửa trong nghiên cứu khoa học. Những khám phá mới nhất về hàm Zeta đang được tiếp tục tạo ra và dự đoán sẽ còn tiếp diễn trong tương la
Hy vọng bài viết này đã giúp bạn hiểu hơn về ứng dụng và tính chất của hàm Zeta và khám phá ra sự quan trọng của nó trong khoa học và thực tiễn.

